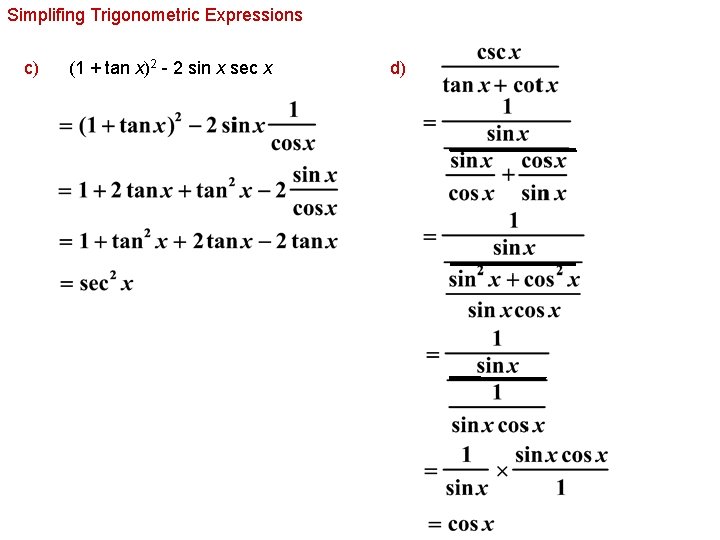
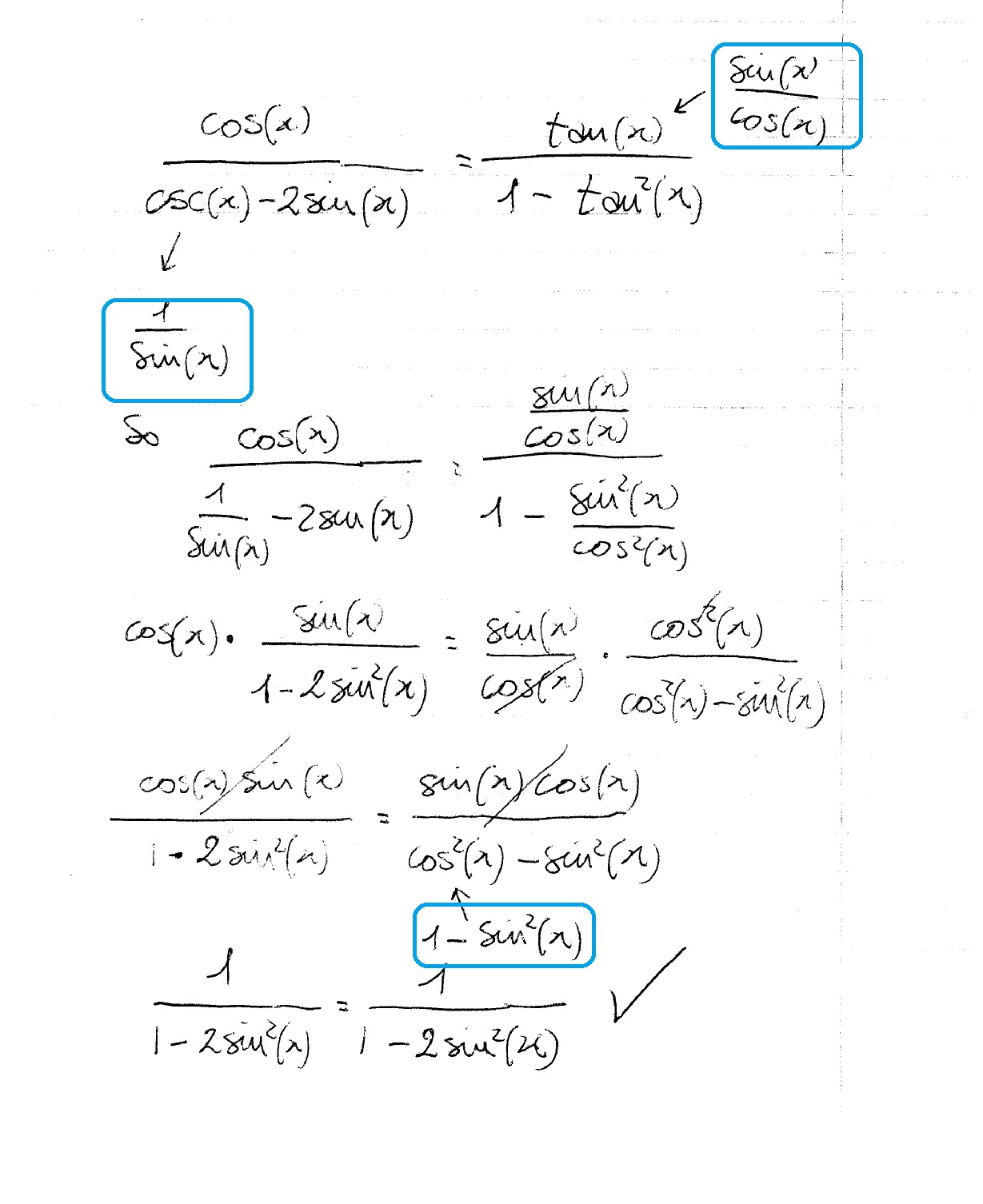
Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes
Tan^-1(2x/1-x^2) formula-No Horizontal Asymptotes No Oblique Asymptotes Vertical Asymptotes x = π2πn x = π 2 π n where n n is an integer Use the form atan(bx−c) d a tan ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a Establish a reduction formula for ∫ tan n ( 2 x) d x My attempt let I n = ∫ tan n ( 2 x) d x, = ∫ tan 2
Tan^-1(2x/1-x^2) formulaのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 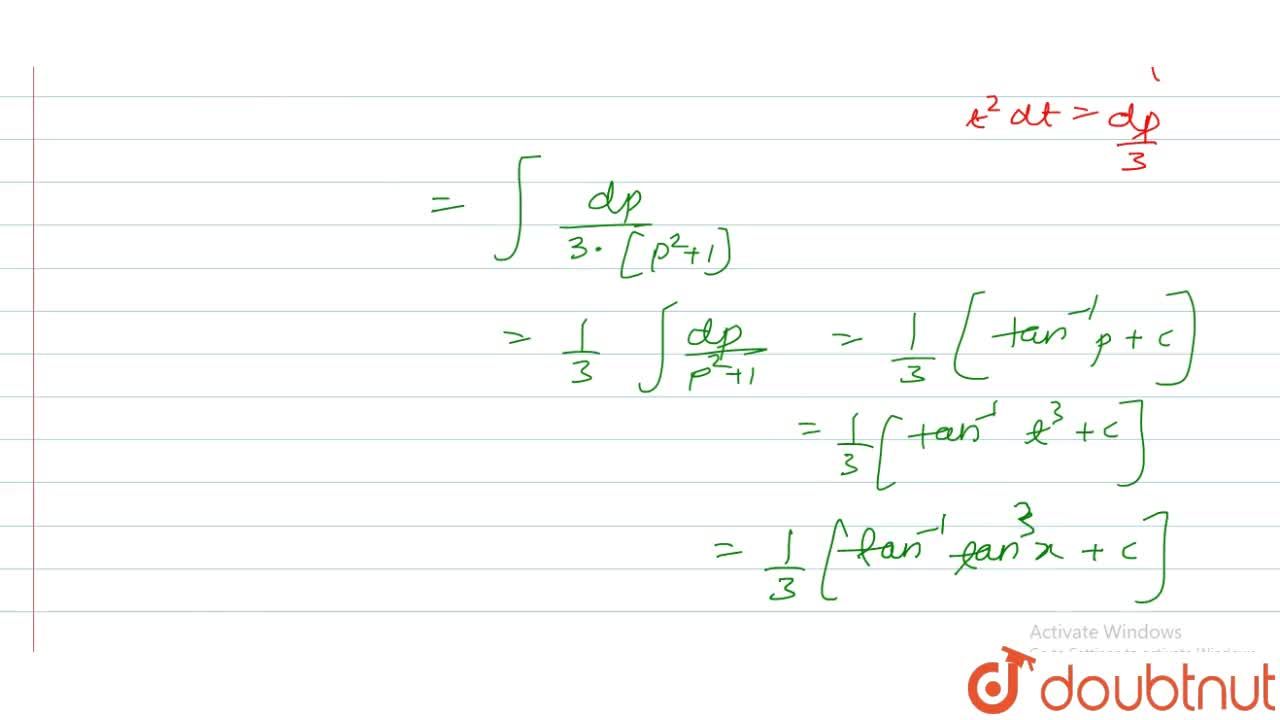 | |
 |  | |
 | 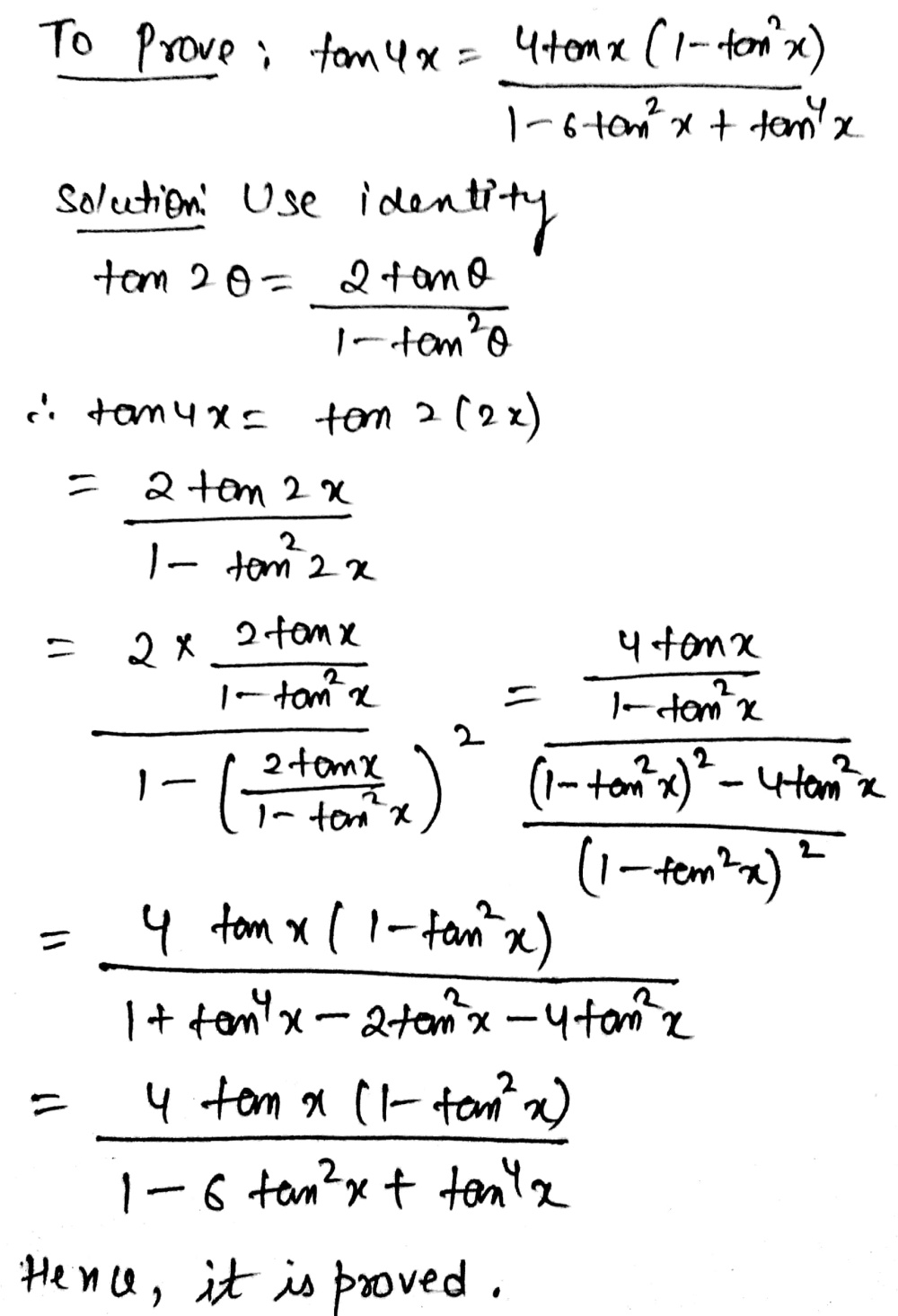 |  |
 |  | 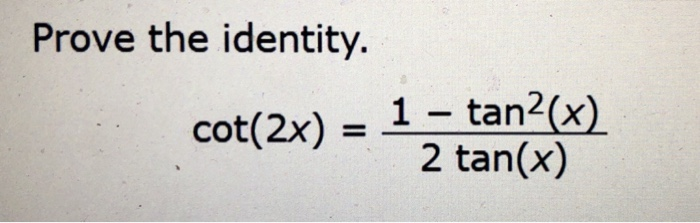 |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
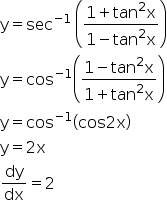 |  | 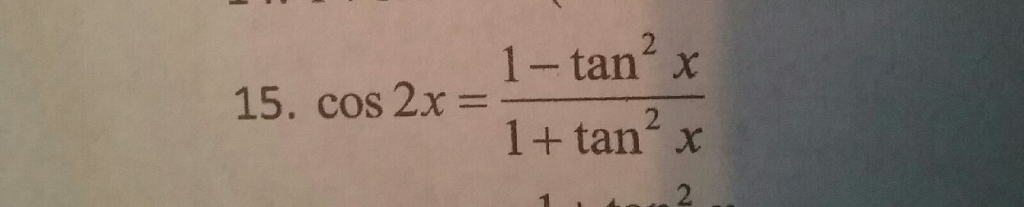 |
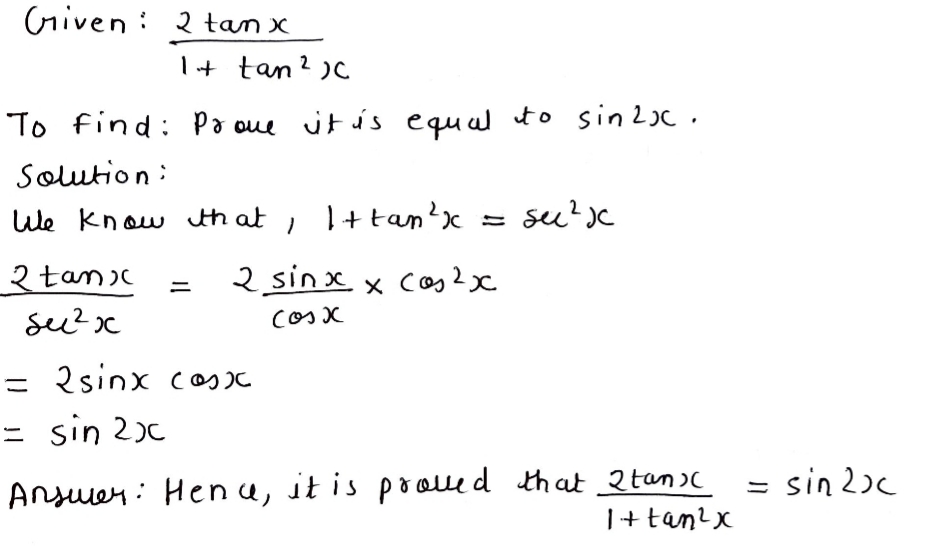 |  | |
 |  | |
 |  |  |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | 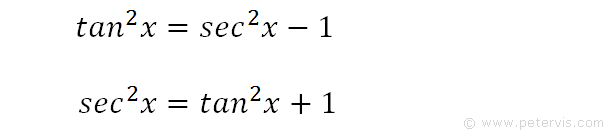 |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
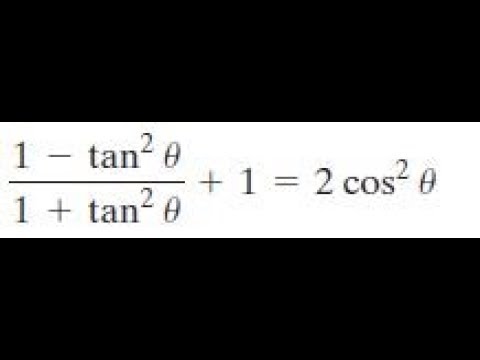 | ||
 | ||
 |  |  |
 | ||
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 | ||
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 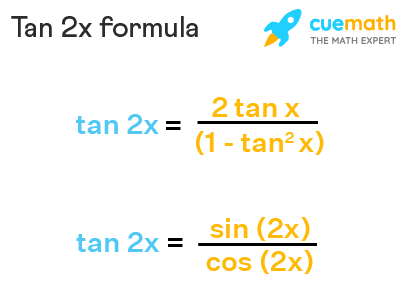 |  |
 | ||
 |  | 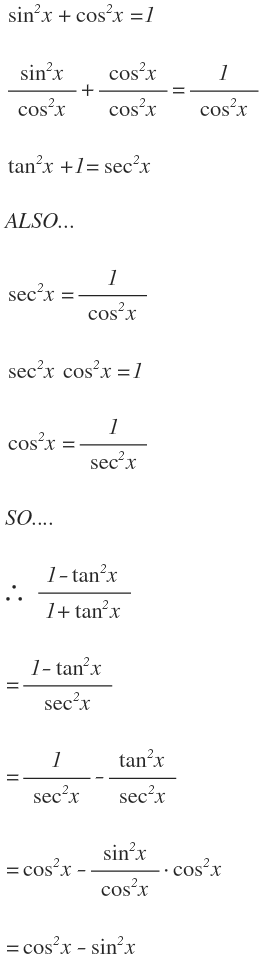 |
 | 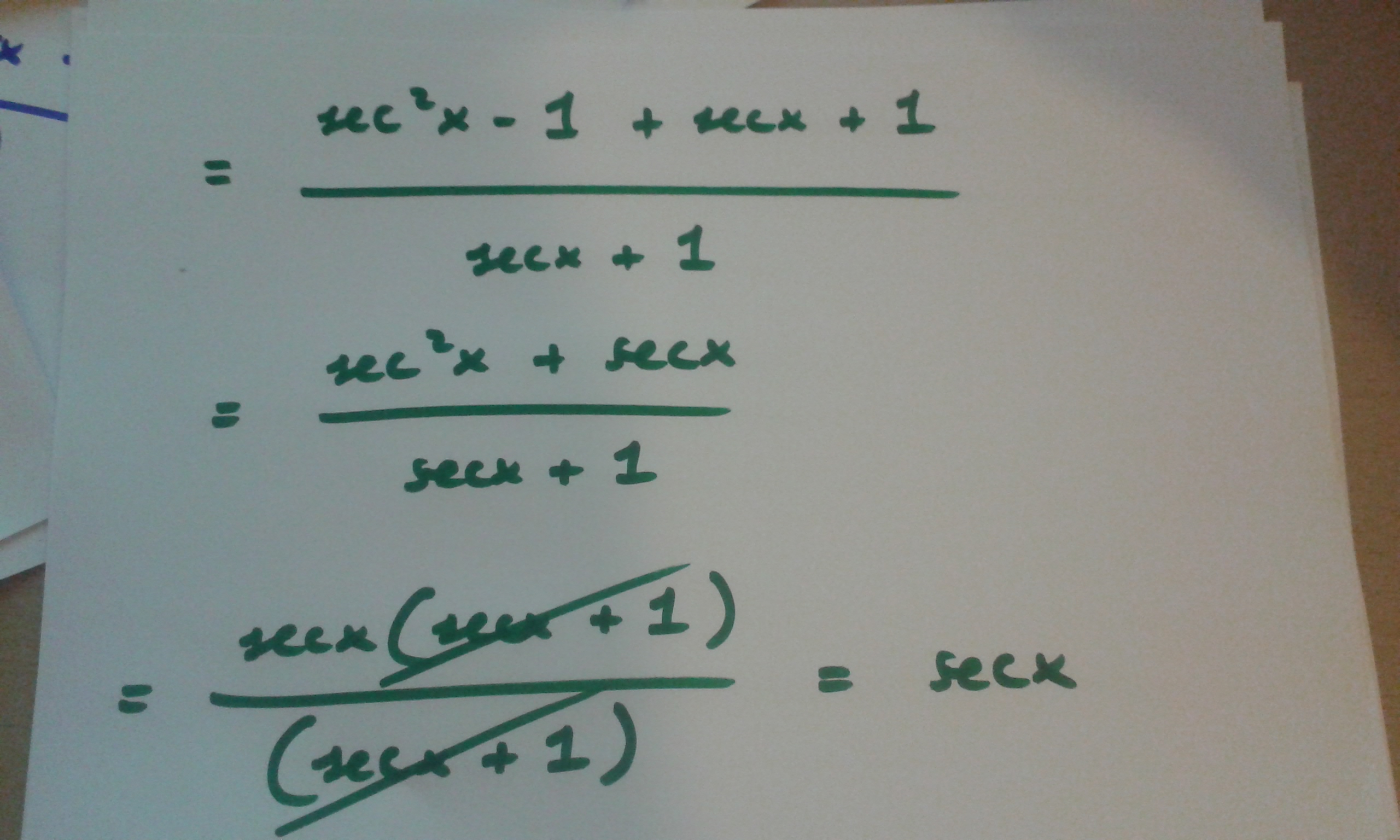 | |
「Tan^-1(2x/1-x^2) formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | .JPG) |
 |  |  |
 |  |
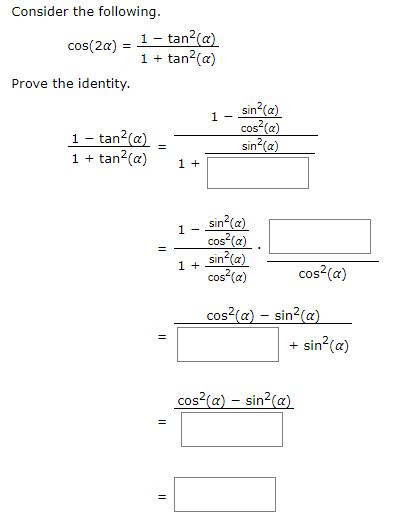
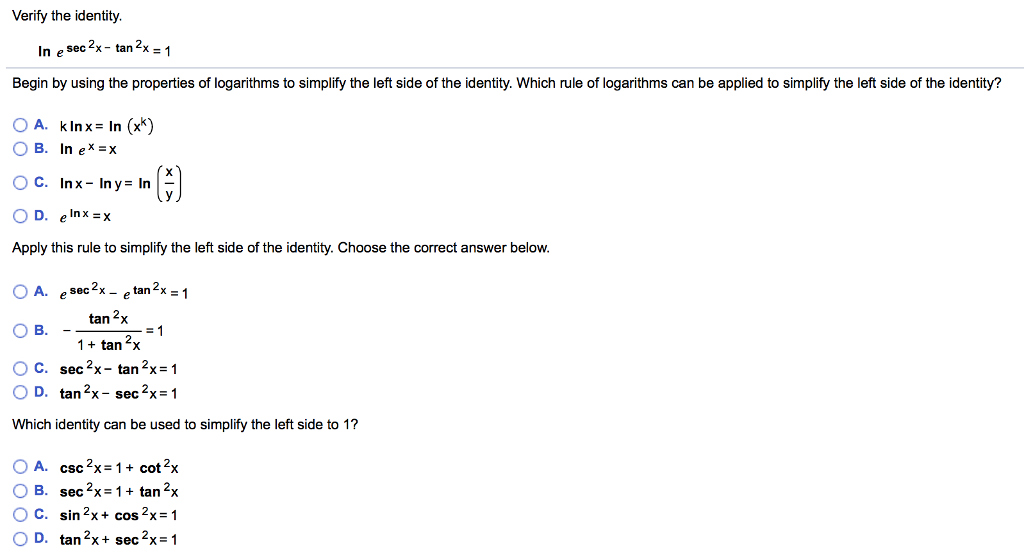
Cos(α β) = cos(α) cos(β) – sin(α) sin(β) cos(α – β) = cos(α) cos(β) sin(α) sin(β) By the way, in the above identities, the angles are denoted by Greek letters The atype letter, "α", is called "alpha", which is pronounced "ALfuh" The btype letter, "β", is= (1 tan 2 x)/(1 tan 2 x) Because tan x = sin x / cos x Hence, we have cos2x = (1 tan 2 x)/(1 tan 2 x) in terms of tan x
Incoming Term: 1-tan^2x/1+tan^2x formula, tan^-1(2x/1-x^2) formula,




0 件のコメント:
コメントを投稿